Home > Robocode

• Introduction
• Installing Robocode
• Running Robocode with RLAI
• Development of a RL Robot for Robocode
  • Radar-Driven Aiming Against a Stationary Opponent (GitHub)
    • Introduction
    • Reward Signal
    • State Features
    • Learning Model and Training
    • Results
  • Radar-Driven Aiming Against a Mobile Opponent (GitHub)
    • Introduction
    • Reward Signal
    • State Features
    • Learning Model and Training
    • Results
  • Evasive Movement
    • Introduction
    • Reward Signal
    • State Features
    • Learning Model and Training
    • Results
  • Integrated Aiming, Firing, and Movement (TBD)

Introduction

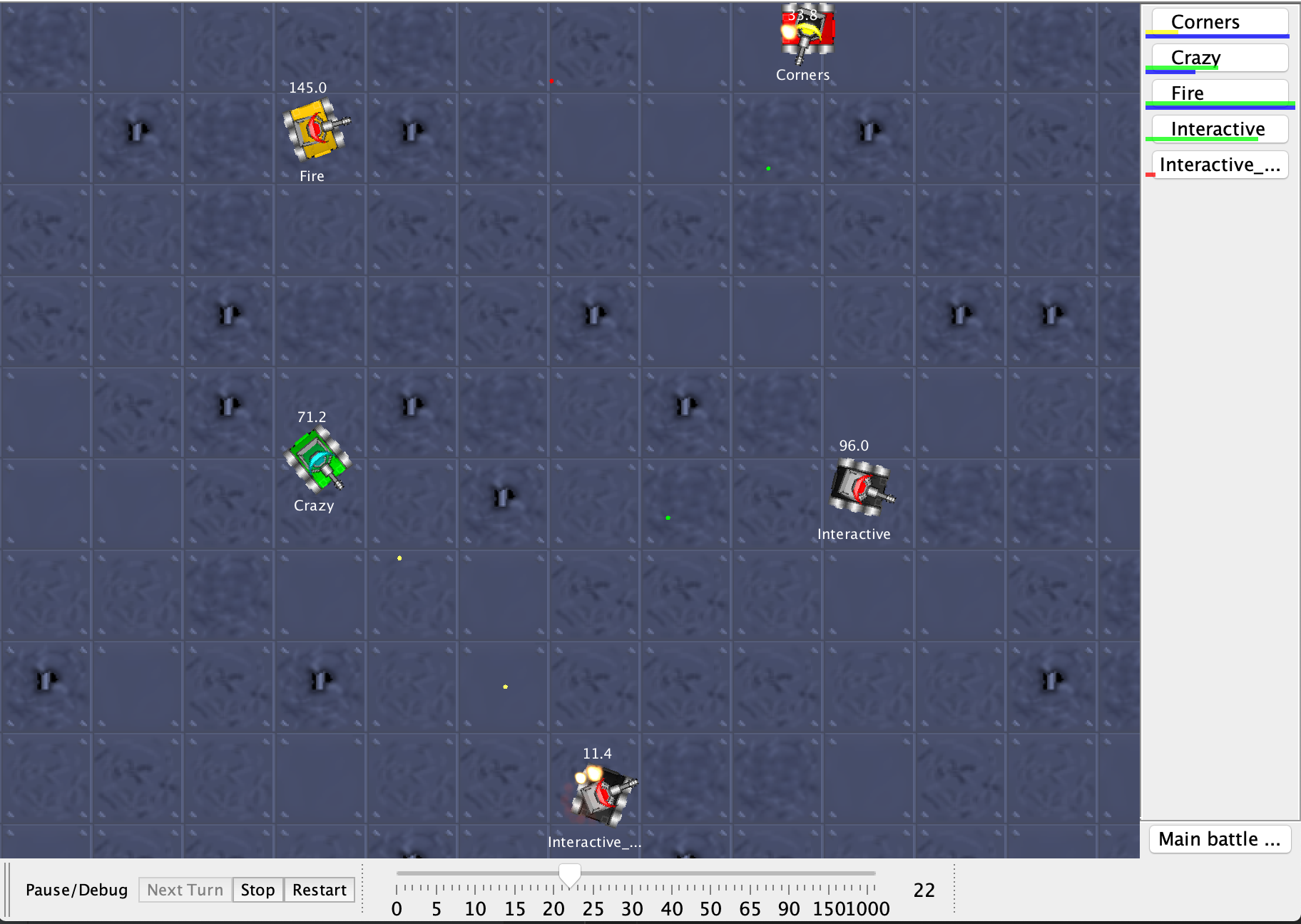Robocode is a programming game in which robot agents are programmed to operate in a simulated battle environment. Full documentation about the game can be found here. Robocode has several features that make it an appealing testbed for reinforcement learning:

• Rich dynamics: The state space is continuous, and each robot has several dimensions of interrelated action, some of which are discrete (fire or not) and some of which are continuous (rotation of the robot, gun, and radar). There are many options for reward functions. The official scoring function is a mixture of many variables, and simpler reward functions can be designed (e.g., bullet hit percentage, robot energy level lost or gained).
• Multi-agent with teaming: Robocode is inherently multi-agent. Teams can be formed, and team members can communicate by passing messages to each other.
• Integration with RLAI: The architecture of Robocode lends itself to integration with RLAI via local network-based exchange of state and action information.

The purpose of this case study is to explore the use of RLAI for learning robot policies.

Installing Robocode

1. Download the Robocode installer here. This is a customized build of Robocode that has been modified to make it compatible with RLAI. This build provides robots with elevated permissions, particularly (1) permission to use TCP (socket) communication with the localhost (127.0.0.1) and (2) permission to perform reflection-based inspection of objects. These permissions are needed to communicate with the RLAI server, and in general they do not pose much of a security risk; however, it is probably a good idea to avoid importing other robots into this installation of Robocode.
2. Run the Robocode installer. Install to a directory such as robocode_rlai.

Running Robocode with RLAI

1. Start the Robocode RLAI environment. This is most easily done using the JupyterLab notebook. There is already a configuration saved in the notebook that should suffice as a demonstration of reinforcement learning with Robocode. Load the configuration and start it.
2. Start Robocode from the directory into which you installed it above. Add a few robots as well as the RlaiRobot, then begin the battle. If this is successful, then you will see the RlaiRobot moving, firing, etc. This is the start of training, so the agent will likely appear random until its policy develops.
3. In order to restart training with different parameters, you will need to first restart the Robocode application and then restart the RLAI environment by killing the command (if using the CLI) or by restarting the JupyterLab kernel. This is a bit tedious but is required to reset the state of each.

Development of a RL Robot for Robocode

The following sections explore the development of a RL robot for Robocode. The approach taken here is incremental and focuses on developing particular skills, rather than addressing the entire behavior policy at once. Each section links to a GitHub commit marking the code and configurations that were used. The layout of each section is as follows:

• Reward Signal: Where we define the reward signal.
• State Features: Where we list the state features per action. A brief explanation is given for the expected learning outcome (ELO) of each feature. Each action has its own intercept term (constant), which quantifies the action’s return when its variables are set to zero. Essentially, we are modeling each action’s value as a linear function of (potentially nonlinear) features, independently of the other actions.
• Learning Model: Where we list other hyperparameters of the value function model.
• Results: Where we discuss results.

Radar-Driven Aiming Against a Stationary Opponent (GitHub)

Introduction

This section develops radar-driven aiming against a stationary opponent. The RL robot is also stationary but is allowed to rotate both its radar (to obtain bearings on the opponent) and its gun (to orient the gun with respect to the opponent’s bearing).

Reward Signal

The reward signal at each time step is defined as the sum of bullet power that has hit the opponent, minus the sum of bullet power that has missed the opponent.

State Features

• Action 1: Turn radar left 5 degrees
  • Feature 1 - Has bearing on opponent (binary) ELO: Rotate radar left when False and do not rotate radar when True.
• Actions 2/3: Turn gun left/right 5 degrees
  • Feature 1 - Has bearing on opponent (binary) ELO: Keep gun stationary when False and rotate gun when True.
  • Feature 2 - Gun is counterclockwise from opponent (binary) ELO: Rotate gun clockwise when True and counterclockwise when False.
• Action 4: Fire
  • Feature 1 - Has bearing on opponent (binary) ELO: Do not fire when False and consider firing when True.
  • Feature 2 - Square root of degree deviation from gun to opponent (continuous) ELO: Only fire gun when sufficiently well aimed.

Learning Model and Training

Key model parameters are listed below:

• SARSA state-action value estimation (n-step=100)
• Discounted (gamma=0.99)
• Epsilon greedy (epsilon=0.2)
• Stochastic gradient descent (step size=0.001)
• Number of Robocode training rounds: 30

The full training command with all parameters is listed below:

rlai train --random-seed 12345 --agent rlai.gpi.state_action_value.ActionValueMdpAgent --gamma 0.99 --environment rlai.core.environments.robocode.RobocodeEnvironment --port 54321 --train-function rlai.gpi.temporal_difference.iteration.iterate_value_q_pi --mode SARSA --n-steps 100 --num-improvements 1000 --num-episodes-per-improvement 1 --num-updates-per-improvement 1 --make-final-policy-greedy True --num-improvements-per-plot 5 --save-agent-path ~/Desktop/robot_agent.pickle --q-S-A rlai.gpi.state_action_value.function_approximation.ApproximateStateActionValueEstimator --epsilon 0.2 --plot-model --plot-model-per-improvements 5 --function-approximation-model rlai.gpi.state_action_value.function_approximation.models.sklearn.SKLearnSGD --loss squared_error --sgd-alpha 0.0 --learning-rate constant --eta0 0.001 --feature-extractor rlai.core.environments.robocode.RobocodeFeatureExtractor

Running this training command in the JupyterLab notebook is shown below:

Results

The policy learned above produces the following Robocode battle:

In the video, the game rate is being manually adjusted to highlight early segments of the first few rounds and then speed through the rest of the battle (see the slider at the bottom). It is clear that the agent has developed a tactic of holding fire at the start of each round while rotating the radar to obtain a bearing on the opponent. Once a bearing is obtained, the gun is rotated accordingly and firing begins when the gun’s aim is sufficiently close. All ELOs seem to be satisfied by this approach.

Radar-Driven Aiming Against a Mobile Opponent (GitHub)

Introduction

This section develops radar-driven aiming against a mobile opponent. The RL robot is stationary but is allowed to rotate both its radar (to obtain bearings on the opponent) and its gun (to orient the gun with respect to the opponent’s bearing). A mobile opponent introduces the following challenges:

• Unreliability of enemy bearings: An enemy bearing obtained at time t is unlikely to be correct at time t+1.
• Coordination of radar and gun rotation: Enemy bearings are obtained by rotating the radar, which will need to be done frequently given the unreliability of enemy bearings. Run rotation will need to be coordinated with radar rotation in order to aim effectively.
• Planning for bullet travel time: Bullets travel at finite speed, so aiming at a mobile opponent will need to account for the enemy’s velocity and distance from the gun.

Reward Signal

The reward signal at each time step is defined as the sum of bullet power that hit the opponent, minus the sum of bullet power that missed the opponent. One difficulty that arose in the current development iteration pertains to reward delay and discounting. Many time steps elapse from the time a bullet is fired until it registers as a hit or miss. It is likely that the robot will take many actions during these intervening time steps, but none of these actions can possibly influence the outcome of the previously fired bullet. If we take the usual approach of discounting the bullet’s reward starting at the time when it hits or misses, then it becomes difficult to construct an appropriate discount. On one hand, we want the time step associated with the bullet firing to receive full credit for the subsequent hit or miss outcome. This would require us to eliminate discounting (i.e., gamma=1.0). On the other hand, we know that actions intervening between the firing of the bullet and the bullet’s hit or miss outcome should receive no credit. This would require us to discount entirely (i.e., gamma=0.0). In the usual discounting approach, we cannot simultaneously assign full credit to the bullet firing action while also assigning zero credit to actions that intervene between firing and the bullet’s outcome. A solution is to move away from the usual discounting approach. The alternative taken here is shown below:

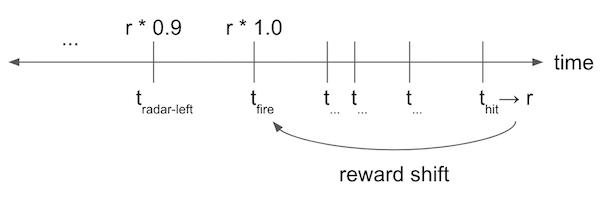
In this alternative, the hit or miss outcome is shifted without discounting to the time at which the bullet was fired. The usual discounting is applied starting at this time step and working backward through actions taken prior to firing.

State Features

The state features described in this section make heavy use of two general concepts that are described below.

• Enemy bearing indicator: This is a binary indication of whether the enemy’s bearing is known. As described in the introduction to this section, one cannot assume (as in the previous development iteration) that the enemy’s bearing will remain reliable after acquisition, since the enemy is moving. Here we only retain the enemy’s bearing for the time step in which it was acquired. If in the next time step the radar has left the enemy, then all binary indications of the enemy’s bearing will be False.

• Aim quality via lateral distance: Aiming the radar or gun usefully (i.e., in a way that will gain positive reward) requires an estimate of where the bullet will arrive in relation to the enemy position. A useful notion here is that of lateral distance. This is depicted below:

  

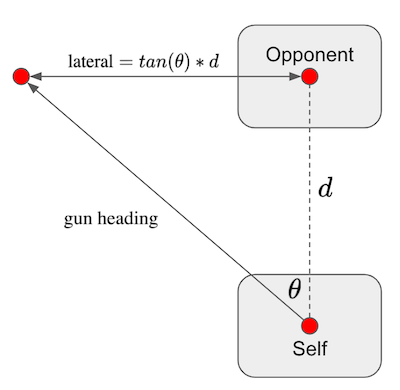
  As shown in the figure, lateral distance is a measure of how far the bullet would be from the opponent given the gun’s heading, the distance to the opponent, and instantaneous arrival of the bullet at its destination. Here, negative distances arrive to the left of the opponent, and positive distances arrive to the right. Of course, the opponent is likely to be moving while the bullet is traveling, but setting this aside for now the lateral distance is a helpful measurement of aim quality. For gun heading values <= -90 degrees and >= +90, the lateral distance is defined to be negative infinity and positive infinity, respectively. We will need to transform lateral distance values in order to use them as state features, for at least two reasons. First, the finite distances are unbounded and are on different scales than other features. Feature scaling causes problems in the selection of the step size for stochastic gradient descent, which is used here. Second, infinite values cannot be used regardless of scaling considerations. Relevant transformations will be explained below.

• Action 1/2: Turn radar left/right 5 degrees
  • Feature 1 - Has bearing on opponent (binary) ELO: Rotate radar either left or right when False and do not rotate radar when True.

  • Feature 2 - Signed squash of lateral distance The lateral distance from the radar to the opponent is transformed to be in [-1.0, 1.0] using the sigmoidal squashing function shown below:

    

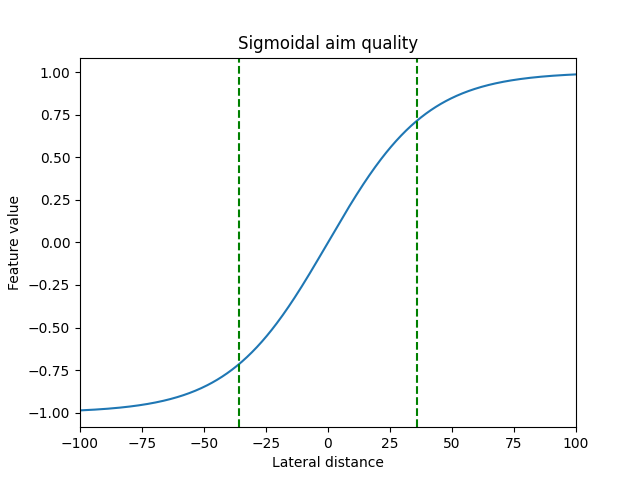
    Dashed reference lines are drawn at -36 and +36, marking the width of Robocode robots. This transformation handles infinite negative and positive values, which converge to -1.0 and +1.0, respectively. ELO: Rotate radar to the right when the squashed value is negative and to the left when the squashed value is positive.

• Action 3/4: Turn gun left/right 5 degrees
  • Feature 1 - Has bearing on opponent (binary) ELO: Keep gun stationary when False and consider rotating gun either left or right when True.
  • Feature 2 - Signed squash of lateral distance (same as for radar, see above).
• Action 5: Fire
  • Feature 1 - Has bearing on opponent (binary) ELO: Do not fire when False and consider firing when True.

  • Feature 2 - Funneled lateral distance For the purpose of deciding whether to fire, it might not help to distinguish left (negative) from right (positive) lateral distance. As such, the lateral distance is funneled as shown below:

    

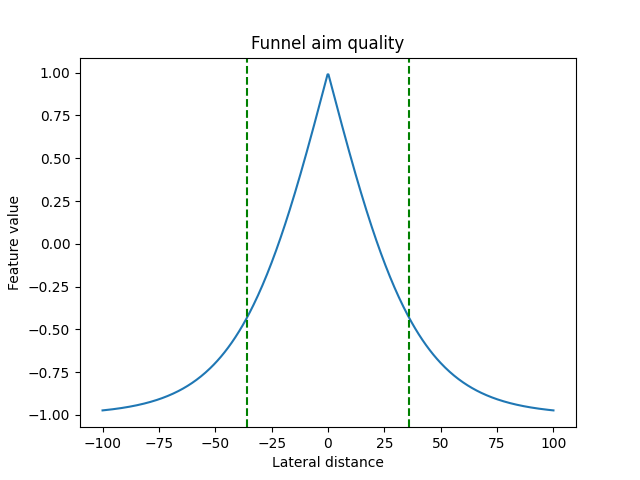
    In a future development iteration, it would be interesting to try shifting the funnel’s peak to be negative or positive to compensate for the opponent’s velocity and distance from the gun. ELO: Only fire gun when sufficiently well aimed.

A useful consequence of transforming lateral distances as described above is that there is no need for an extra step of feature standardization, which was used in the previous iteration but found to be unnecessary here.

Learning Model and Training

Key model parameters are listed below:

• SARSA state-action value estimation (n-step=500)
• Discounted (gamma=0.9)
• Epsilon greedy (epsilon=0.15)
• Stochastic gradient descent (step size=0.0005)
• Number of Robocode training rounds: 100

The full training command with all parameters is listed below:

rlai train --save-agent-path ~/Desktop/robot_agent.pickle --random-seed 12345 --agent rlai.gpi.state_action_value.ActionValueMdpAgent --gamma 0.9 --environment rlai.core.environments.robocode.RobocodeEnvironment --port 54321 --train-function rlai.gpi.temporal_difference.iteration.iterate_value_q_pi --mode SARSA --n-steps 500 --num-improvements 100 --num-episodes-per-improvement 1 --num-updates-per-improvement 1 --make-final-policy-greedy True --num-improvements-per-plot 5 --q-S-A rlai.gpi.state_action_value.function_approximation.ApproximateStateActionValueEstimator --epsilon 0.15 --plot-model --plot-model-per-improvements 5 --function-approximation-model rlai.gpi.state_action_value.function_approximation.models.sklearn.SKLearnSGD --loss squared_error --sgd-alpha 0.0 --learning-rate constant --eta0 0.0005 --feature-extractor rlai.core.environments.robocode.RobocodeFeatureExtractor

Running this training command in the JupyterLab notebook is shown below:

Boxplots of the model coefficients for each action are shown below:

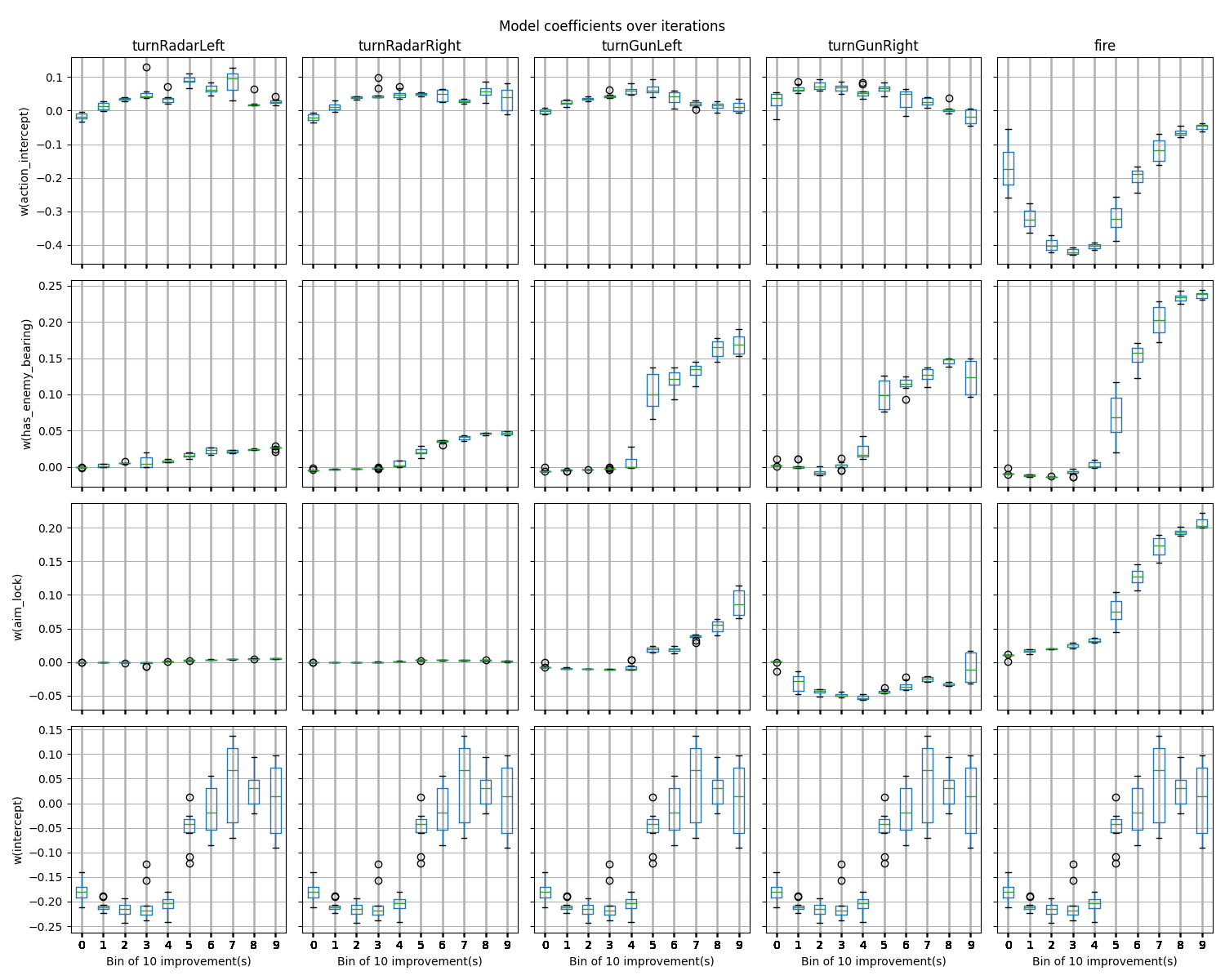
In the boxplots above, the y-axes show feature weights, and the x-axes bin the training iterations (battle rounds) into groups of 10. The first 10 rounds are in bin 0, and the final 10 rounds are in bin 9. A few observations above these boxplots:

• Obtaining a bearing on the opponent (second row) increases the value of turning the gun left or right as well as firing.
• The aim quality features described above are shown in the third row where they are named aim_lock. Note that the signed sigmoidal feature used for turning the gun has a positive weight for turning the gun left. This is interpreted as assigning negative value to turning the gun left when the gun is already left of the opponent, whereas the value of turning the gun left when the gun is right of the opponent is positive. The weight of this feature for turning the gun right is generally negative, reversing the interpretation. All of this makes sense.
• The aim quality feature for firing (row three, final column) is strongly positive.

In general, these feature weights are consistent with the ELOs and intuition.

Results

The policy learned above produces the following Robocode battle:

Having experimented with the features, model parameters, and learned policies obtained in this iteration, it appears that most of the ELOs are satisfied. However, the radar was not expected to exhibit the behavior shown above, where it rotates continuously. The radar was expected to stay fixated on the opponent, as this would provide the most up-to-date bearings to the opponent. Training was performed several times, and this was always the successful policy that emerged. What’s going on? The answer likely lies in the specification of the reward signal, which instructs the agent to maximize bullet hits and minimize bullet misses. This objective does not differentiate the policy shown in the preceding video from an alternative in which the radar remains fixated continuously on the opponent. If the reward were redesigned to emphasize bullet hits per turn, then the alternative (radar fixation) would likely be favored because it would enable accurate, high-rate firing.

Primary points of future development:

• Shift the aim quality feature for firing (i.e., the funnel’s peak) left or right to compensate for the opponent’s velocity and distance from the gun.
• Redefine the reward to emphasize hits per turn.

Evasive Movement

Introduction

This section develops evasive movement against a stationary opponent who is actively tracking and firing. The RL robot is mobile but is not allowed to rotate its gun or fire. Moving unarmed against a firing opponent introduces the following challenges:

• Obstacle avoidance: Obstacles include boundary walls as well as the opponent robot. The RL robot will need tactics for avoiding obstacles and navigating away or around them when they are encountered.
• Bullet avoidance: The RL agent will need to move such that it is difficult for the opponent to aim and fire effectively.
• Bullet escape: The opponent will inevitably score bullet hits. Success will depend partly on how the RL agent responds to bullet hits.

Reward Signal

The reward signal at each time step is 1.0 if no bullet hit the RL robot, and it is -10.0 if a bullet did hit the RL robot. Why the asymmetry? The enemy’s rate of fire is limited by Robocode physics, which dictate that each bullet firing event heats the gun. The enemy’s gun will not fire beyond a heat threshold, until it cools below the threshold per the cooling rate. Because the enemy’s rate of fire is limited, few bullets can possibly hit the RL agent relative to the number of turns. Thus, if the reward signal is symmetric with 1.0 (for each turn without a hit) and -1.0 (for each turn with a hit), then it is easy for returns to be dominated by positive values even when the enemy is aiming, firing, and hitting the RL robot very effectively. Using the asymmetric reward compensates for the enemy’s limited rate of fire, making hits much more prominent within the returns. I didn’t explore alternatives to -10.0, as it seemed to work without much experimentation.

State Features

• Actions 1/2: Move ahead/back 25 pixels.
  • Feature 1 - Has bearing on opponent (binary) ELO: Consider moving if Features 6 and 7 have values indicating that movement would be useful (see below).
  • Feature 2 - Cumulative hit-by-bullet power (continuous) Each bullet inflicts a certain about of damage (e.g., reduction of energy by four points for standard bullets). This feature tracks the cumulative decaying bullet power that has hit the RL robot. In each turn, the bullet power that just hit the RL robot is added to the cumulative total, and the resulting total decays by 0.9 on each subsequent turn. ELO: Turn and flee when this feature is large, and continue on the current trajectory when this feature is near zero.
  • Feature 3 - The action collides the RL robot with the opponent robot (binary) ELO: Take the action when False and move in the opposite direction when True.
  • Feature 4 - The action can be completed with a remaining buffer of 100 pixels to the boundary (binary) ELO: Take the action when True and take a different action when False.
  • Feature 5 - The action will continue to take us farther from our previous location (binary) Given our previous and current locations, this is True if the action will take us even farther from our previous location. This feature was critical in getting the RL robot to string together extended sequences of forward and backward navigation. Without it, the agent had no way to explain the goodness of moving forward following a previous forward movement. ELO: Move in whatever direction continues the trajectory.

  • Feature 6 - Bearing is clockwise-orthogonal to enemy (continuous) The funneled, shortest degree change from the RL robot’s current heading to the bearing that would be clockwise-orthogonal to the opponent’s direction. This feature is depicted in the following figure:

    

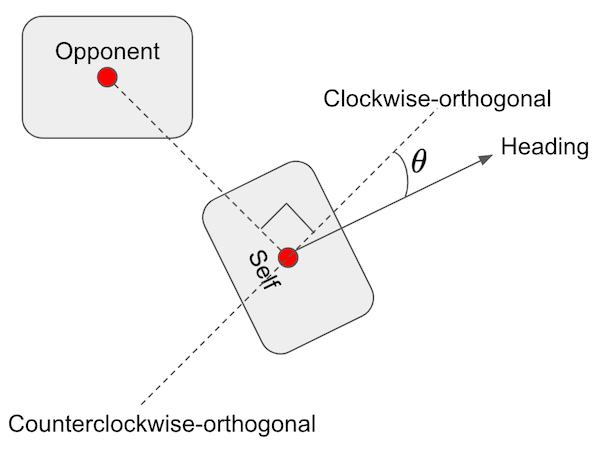
    In the figure, two line segments (clockwise-orthogonal and counterclockwise-orthogonal) are drawn at right angles to the line segment that connects the opponent to the RL robot. The RL robot’s heading is shown as a degree offset of theta from the clockwise-orthogonal line segment. This value of theta is funneled per the earlier figure, and the funneled value is used as the value for this feature. This feature value is maximized when movement ahead or back would generate the greatest angular velocity of the line segment connecting the two robots. ELO: Movements ahead and back are likely to be useful to the extent that they make aiming more difficult for the enemy, that is, when the value of this feature is maximized.

  • Feature 7 - Bearing is counterclockwise-orthogonal to enemy (continuous) Similar to the previous feature, except that it is with respect to the counterclockwise-orthogonal bearing (see the previous figure).
• Actions 3/4: Turn left/right 10 degrees.
  • Feature 1 - Has bearing on opponent (binary) ELO: Do not turn when False and consider turning either left or right when True.
  • Feature 2 - Bearing is clockwise-orthogonal to enemy (continuous) (same as Feature 6 for ahead/back)
  • Feature 3 - Bearing is counterclockwise-orthogonal to enemy (continuous) (same as Feature 7 for ahead/back)
• Actions 5/6: Turn radar left/right 5 degrees.
  • (same features as described above for aiming)

Learning Model and Training

The full training command with all parameters is listed below:

rlai train --random-seed 12345 --agent rlai.core.environments.robocode.RobocodeAgent --gamma 0.9 --environment rlai.core.environments.robocode.RobocodeEnvironment --port 54321 --train-function rlai.gpi.temporal_difference.iteration.iterate_value_q_pi --mode SARSA --n-steps 100 --num-improvements 10000 --num-episodes-per-improvement 1 --num-updates-per-improvement 1 --epsilon 0.15 --q-S-A rlai.gpi.state_action_value.function_approximation.ApproximateStateActionValueEstimator --plot-model --plot-model-bins 10 --plot-model-per-improvements 100 --function-approximation-model rlai.gpi.state_action_value.function_approximation.models.sklearn.SKLearnSGD --loss squared_error --sgd-alpha 0.0 --learning-rate constant --eta0 0.001 --feature-extractor rlai.core.environments.robocode.RobocodeFeatureExtractor --make-final-policy-greedy True --num-improvements-per-plot 50 --save-agent-path ~/Desktop/robot_agent_move.pickle

Results

The policy learned above produces the following Robocode battle:

A few things are worth noting about the RL robot’s policy:

• It strings together long sequences of ahead or back movement (see ahead/back Feature 5 above).
• The RL robot turns when hit by bullets but then continues with ahead/back movement (see ahead/back Feature 2 above).
• An ahead/back sequence terminates when the RL robot nears a boundary, and the RL robot reverses direction (see ahead/back Feature 4 above).
• It is not uncommon for the movement-only RL robot to defeat this particular enemy, as the former often settles into a movement pattern like the one shown in the video. The enemy’s aim is not properly calibrated for a moving target at long range, and the RL agent’s repeated direction reversals incur little if any damage.

Integrated Aiming, Firing, and Movement (TBD)